Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Exercícios e Problemas - Ex. 48

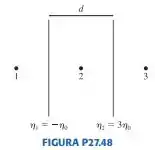
Suponha que você segure duas grandes folhas de plástico frente à frente, espaçadas uma da outra por d, conforme mostra a FIGURA P27.48. Atritando uma delas com lã e a outra com seda, você consegue obter, sobre a superfície de uma das folhas, uma densidade superficial uniforme de carga η 1 = - η 0 , e sobre a outra, outra densidade superficial uniforme de carga η 2 = + 3 η 0   .Qual é o vetor campo elétrico nos pontos 1, 2 e 3?

Passo 1

Faaaaaala, galera... Tranquileba??

Vamos definir o campo elétrico a uma distância z do disco, assim:

Sabemos pela definição de campo que:

E i = 1 4 π ε 0 ∫ d q r ' 2

Vemos que o campo em x e y se cancelam, logo:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ d q r ' 2 cos ⁡ θ

Sabemos que a densidade de carga é dada por:

η = q A

d q = η   d A = η d π r 2 = η 2 π r   d r

Assim:

E → =   1 4 π ε 0 ∫ η 2 π r d r r ' 2 cos ⁡ θ

Para:

r ' = r 2 + z 2 1 2

E:

cos ⁡ θ = r r ' = r r 2 + z 2 1 2

Assim ficando:

E → = E z cos ⁡ θ = 1 4 π ε 0 ∫ η   2 π r d r r 2 + z 2   r r 2 + z 2 1 2 = η z 2   ε 0 ∫ r r 2 + z 2 3 2   d

Integrando de 0 ≤ r ≤ R , temos que o campo sobre um disco é:

E → = η 2 ε 0 1 - z R 2 + z 2

Para z ≫ R :

E → = η 2 ε 0 1 - 1 R 2 z 2 + 1

E = η 2 ϵ 0

Uuuufa! Essa cansou em..., mas agora podemos achar a resposta

Passo 2

Para o ponto 1)

O princípio da superposição nos diz que:

E p o n t o 1 = E f o l h a 1 + E f o l h a 2

E p o n t o   1 → = η 0 2 ϵ 0   i v e r s o r + - 3 η 0 2 ϵ 0     i v e r s o r = - η 0 ϵ 0   i v e r s o r

Passo 3

Para o ponto 2)

Pela superposição:

E p o n t o 2 = E d i r e i t a + E e s q u e r d a

E p o n t o 2 = - η 2 ϵ 0 + - 3 η 0 2 ϵ 0  

E p o n t o 2 → = - 2 η 0 ϵ 0   i v e r s o r

Para o ponto 3)

Similar ao ponto 1, mas de valor positivo pela inversão, logo:

E p o n t o 3 → = + η 0 ϵ 0   i v e r s o r

Resposta

Para 1)

E p o n t o   1 → = - η 0 ϵ 0   i v e r s o r

Para 2)

E p o n t o 2 → = - 2 η 0 ϵ 0   i v e r s o r

Para 3)

E p o n t o 3 → = + η 0 ϵ 0   i v e r s o r

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um anel estacionário de raio a está no plano y z e tem uma carga positiva uniforme Q . Uma pequena partícula com massa m e carga negativa - q está localizada no centro do anel. (a) Mostre que se x ≪ a
Se o raio do anel do Problema 80 for duplicado, mantendo a mesma densidade linear de carga, a frequência de oscilação da partícula varia? Se a resposta for positiva, por qual fator ela varia?
As cargas Q e q do problema 80 são + 5,00μ C e - 5,00μ C , respectivamente, e o raio do anel é 8,00c m . Quando a partícula é levemente deslocada na direção x ela oscila em torno de sua posição de equ
Um condutor em forma de anel com raio a=2,5 cm possui uma carga positiva Q=+0,125 nC uniformemente distribuída ao longo do anel, como indica a figura 21.24. O centro do anel está na origem O do sistem
Uma carga de - 6,5n C está uniformemente distribuída sobre a superfície da face de um disco não condutor de raio 1,25c m .(a) Determine o módulo, a direção e o sentido do campo elétrico que esse disco