Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 33.Exercícios e Problemas - Ex. 15
A intensidade do campo magnético sobre o eixo de um pequeno ímã, a do mesmo, é de .
- Qual é o momento de dipolo magnético do ímã?
- Qual é a intensidade do campo sobre o eixo a 15 cm do ímã?
Passo 1
Faaaaaala, galera... Tranquileba??
Precisamos definir primeiro a equação do dipolo magnético. Assim, achemos o campo magnético em função de seu dipolo. Cola comigo!
Seja uma espira ideal:
Então:
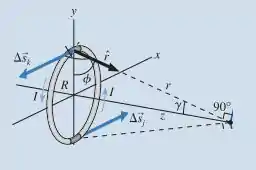
Vemos que as componentes em x e y se cancelam, sobrando somente em z.
Sabendo que a lei de bio-savart é:
Veja que:
Assim:
E que:
E também:
Assim ficando:
Integrando sobre toda a espira:
Concluímos que o campo magnético sobre uma espira é:
Tomando à parte:
Tomando a aproximação de que
Assim, tomando o campo magnético na espira para :
Multiplicando por em cima e em baixo:
Sabemos que
E é chamado de momento de dipolo magnético . Assim:
Com esse “insight” nem precisa mais de mim, né?! Mas se gosta de mim, cola pro próximo passo!
Passo 2
Gostou né?! huehue
Brincadeiras à parte, pede-se , então:
Onde A é ampere, para não se confundir.
Passo 3
Para b)
Tendo já o momento de dipolo magnético, sendo constante em todo o percurso, em :
Resposta
Para a)
Para b)