O interruptor da Figura P23.43 está aberto quando t
Passo 1
E aiii gente, tudo bom com vocês?
Então vamos resolver essa questão bem legal aqui e passo a passo pra gente tirar 10 na provinha!
Vamo lá!
Vamos nomear as correntes conforme mostrado. Pelas leis de Kirchhoff:
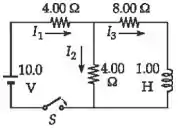
De (1) e (2):
E (3) se torna:
Que pode ser comparada com a equação geral e sua solução . Então temos:
Passo 2
Letra a:
Passo 3
Letra b: