Isolamento em mamíferos. Animais em climas frios geralmente dependem de duas camadas de isolamento: uma camada de gordura do corpo ( condutividade térmica igual a 0,20 W /m · K) cercada por uma camada de ar envolvida dentro da pele ou mais abaixo. Podemos modelar um urso negro (Ursus americanus) como uma esfera com 1,5 m de diâmetro tendo uma camada de gordura de 4,0 cm de espessura. (Na realidade, a espessura varia com a estação, mas estamos interessados na hibernação, quando a camada de gordura é mais grossa.) Nos estudos sobre hibernação de ursos, descobriu-se que a camada da superfície externa da pele está a 2, 7 °C durante a hibernação, enquanto a superfície interna da camada de gordura está a 31,0 °C. (a) Qual é a temperatura no limite entre gordura e interior da pele para que o urso perca calor a uma taxa de 50,0 W? (b) Qual deverá ser a espessura da camada de ar (contida dentro da pele)?
Passo 1
Fala galera, bora lá! Vimos neste capítulo que a equação para transferência de calor é dada por:
Passo 2
Modelaremos esse problema de forma similar ao problema 17.13 resolvido. De forma a esclarecer melhor observe a figura abaixo esquematizando o urso:
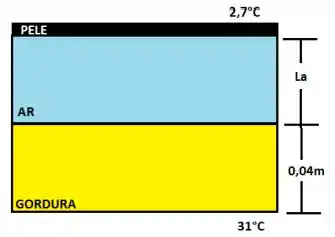
Passo 3
Para resolvermos este problema devemos primeiramente identificar que há transferência de calor entre a camada de ar e a camada de gordura do urso. Assim usaremos a equação dada acima de forma que as transferências de calor entre as camadas sejam iguais. Por isso fazemos o seguinte passo:
Vale lembrar que as unidades de temperatura devem ser transformadas para Kelvin.
Passo 4
(a) Primeiramente simplificamos a área, pois as áreas de contato entre as duas camadas são iguais. Em seguida, do lado direito da equação obtemos:
Portanto a temperatura limite entre a gordura e a pele é:
Passo 5
(b) Resolvendo o lado esquerdo, substituindo o valor da temperatura encontrado interiormente da equação obtemos:
Resposta
- Para manter o urso perdendo uma taxa de 50 W nas condições fornecidas, deve-se ter uma espessura de ar de