O isopor tem densidade de . Qual é a massa máxima que pode ser pendurada a uma esfera de isopor com de diâmetro, na água, sem afundá-la? Suponha que o volume da massa pendurada seja desprezível comparado ao da esfera
Passo 1
Bom! A fórmula do empuxo é dada por...
E do enunciado, tiramos os seguintes dados mais importantes...
Vamos começar fazendo um diagrama de corpo livre pra bola... Se a bola está completamente submersa, então provavelmente teremos a seguinte situação...
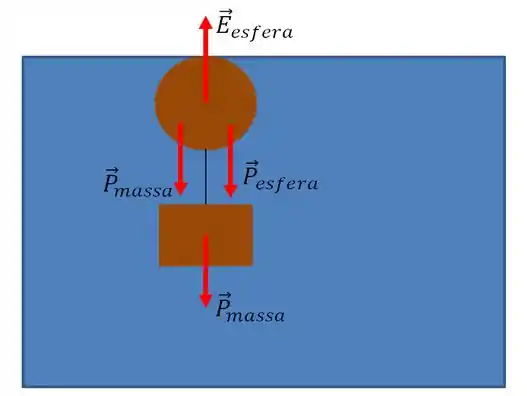
Vamos então, fazer nossa análise!
A força de tensão agindo sobre a massa que vai ser conectada a esfera de isopor vai ser a força peso da massa...
Logo, como todo o sistema está em equilíbrio, a equação para a esfera de isopor vai ser dada por...
Substituindo ...
Obtemos a equação geral do sistema!
Passo 2
O que a gente quer saber, é o valor da massa que deve ser conectada à esfera.
Bem! O peso dessa massa é dado por...
O peso da esfera de isopor, por sua vez, é dado por...
Uma vez que sabemos o valor da densidade da esfera e tratando ela como uma esfera, então sua massa será dada por...
E então, ficamos com...
Passo 3
Por último, falta achar o empuxo agindo sobre a esfera. Ele é dado pela seguinte fórmula...
Como a esfera está completamente imersa na água, então...
O empuxo ficará assim...
Pronto! Já tá tudo no esquema! Agora é só substituir na relação abaixo...
Isolando :
E substituindo os valores numéricos...
Obtemos o valor da massa que deve ser conectada à esfera!