Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 52
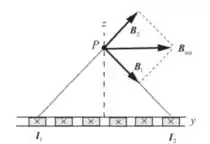
Uma lâmina fina e condutora no plano z=0 conduz corrente na direção -x (Figura 27-58a). A lâmina se estende indefinidamente em todas as dirigées e a corrente está uniformemente distribuída. Para determinar a direção do campo magnético no ponto P considere o campo devido apenas como correntes e nas duas faixas estreitas mostradas. As faixas são idênticas e
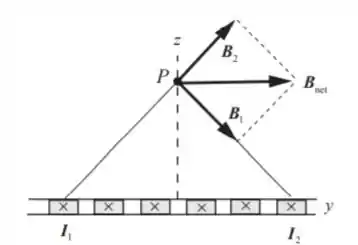
- Quais são a direção e o sentido do campo magnético no ponto P devido a apenas a e ? Explique sua resposta através de um esboço.
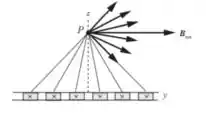
- Quais são a direção e o sentido do campo magnético no ponto P devido a lâmina inteira? Explique sua resposta.
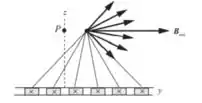
- Quais são a direção e o sentido do campo em um ponto a direita do ponto P (onde y )? Explique sua resposta
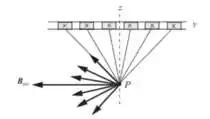
- Quais são a direção e o sentido do campo em um ponto abaixo da lâmina (onde )? Explique sua resposta usando um esboço.
- Aplique a lei de Ampére na curva retangular (Figura 27-58b) para mostrar que a intensidade do campo magnético no ponto P e dada por onde é a corrente por unidade de comprimento ao longo do eixo y.
Passo 1
Nós podemos usar uma regra da mão direita para determinar a direção do campo magnético nos pontos acima e abaixo da folha infinita de corrente nas letras a, b e c. Na letra d, podemos avaliar em torno do caminho especificado e igualá-lo a e resolver para B.
Letra a:
Como seus componentes verticais se cancelam em P, o campo magnético aponta para a direita (ou seja, na direção y).
Passo 2
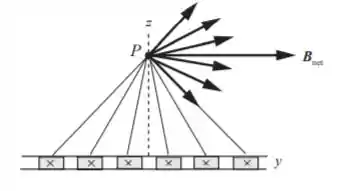
Letra b:
Os componentes verticais do campo se cancelam em pares. O campo magnético está na direção +y.
Passo 3
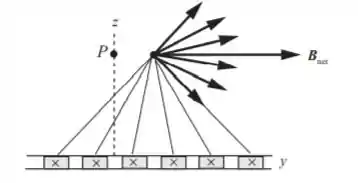
Letra c:
O campo magnético está na direção +y. Este resultado segue dos mesmos argumentos que foram usados em (a) e (b).
Passo 4
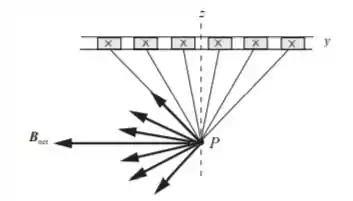
Letra d:
Abaixo da folha o campo magnético aponta para a esquerda; ou seja, na direção -y. Os componentes verticais se cancelam em pares.
Passo 5
Letra e:
Vamos expressar no sentido anti-horário, para o determinado caminho:
Para os caminhos perpendiculares à folha, B e dl são perpendiculares um ao outro e:
Para os caminhos paralelos à folha, B e dl estão na mesma direção e:
Substituindo na equação (1) e simplificando, temos:
Resolvendo para B, temos:
