Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 32.1 - Ex. 91
Uma lente convergente com distancia focal de 10 cme usada para obter uma imagem que tem o dobro da altura do objeto. Determine as distancias objeto e imagem se(a)a imagem deve ser direita e(b)a imagem deve ser invertida.Desenhe um diagrama de raios para cada caso.
Passo 1
Podemos usar as equações de lente fina e de ampliação para obter equações simultâneas que podemos resolver para encontrar as distâncias da imagem e do objeto para as duas situações descritas na definição do problema.
Letra a:
Use a equação da lente fina para relacionar as distâncias da imagem e do objeto à distância focal da lente:
Como a imagem é duas vezes maior que o objeto:
Substitua por para obter:
Passo 2
Letra b:
Se a imagem estiver invertida, então:
Passo 3
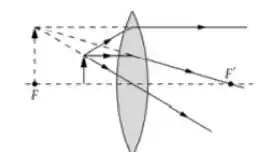
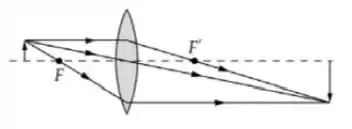
Os diagramas de raios para (a) (esquerda) e (b) (direita) seguem:
