Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Eletromagnetismo- Ed: 5º - Capítulo 19.Problemas - Ex. 71
Uma linha de carga com uma densidade uniforme de se encontra ao longo da linha em , entre os pontos com coordenadas e . Encontre o campo elétrico criado na origem.
Passo 1
Antes de começar a resolver o problema, é fundamental fazer um desenho bem bonito para entender bem o que tá acontecendo:
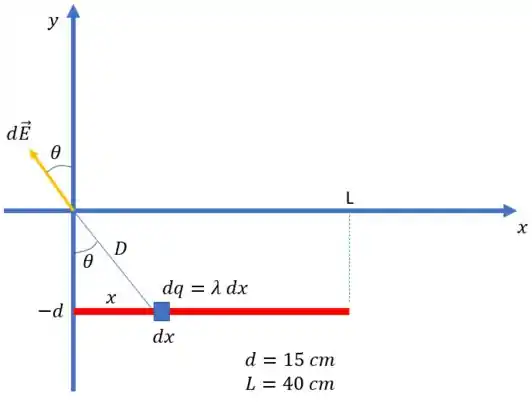
Desenhei o fio em vermelho com entre . Para achar o campo elétrico na origem, pegamos um elemento infinitesimal de fio com carga , onde é a densidade linear de carga no fio. O módulo do campo infinitesimal produzido por esse elemento de fio é
Passo 2
Para achar o vetor , temos que fazer a decomposição usando o ângulo :
Mas observe que
Assim,
Note também que
Desta forma,
Para finalizar, basta integrar em entre e :
Passo 3
A primeira integral é tranquila de calcular fazendo a substituição , de modo que
Assim,
Portanto,
Já para a segunda integral, fazemos a substituição , com
Portanto, fazendo as alterações nos limites de integração:
Essa integral é fácil de fazer:
Só lembrando:
Logo,
Com isso, a segunda integral fica
Passo 4
Agora que temos as integrais calculadas, podemos escrever
Ou ainda,
Só falta substituir os valores e fazer as contas:
Portanto,