Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Oscilações, Ondas e Termodinâmica- Ed: 5º - Capítulo 16.Problemas - Ex. 54

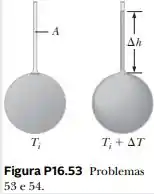
Um líquido com um coeficiente de expansão volumétrica β enche uma concha esférica de volume V (Fig. P16.53). A concha e o capilar aberto de área A projetada a partir do topo da esfera são feitos de um material com coeficiente de expansão linear médio a . O líquido está livre para expandir para dentro do capilar. Supondo que a temperatura aumenta em Δ T , encontre a distância Δ h que o líquido sobe no capilar.

Passo 1

Falaaaaaaaaaaaaaaaa Tribuxo?

Bora resolver mais uma questão!?

Vamos usar:

Δ V = β V i Δ T

Colocando V i em evidência:

V f = V i 1 + β Δ T

Podemos escrever:

V f = V i 1 + 3 α Δ T + A ⋅ 1 + 2 α ⋅ Δ T ⋅ Δ h

Temos:

V i 1 + β Δ T = V i 1 + 3 α Δ T + A ⋅ 1 + 2 α ⋅ Δ T ⋅ Δ h

Passo 2

Isolando Δ h :

Δ h = V i 1 + β Δ T - V i 1 + 3 α Δ T A ⋅ 1 + 2 α ⋅ Δ T

  Δ h = V i + V i β Δ T - V i - V i 3 α Δ T A ⋅ 1 + 2 α ⋅ Δ T

Δ h = V i β Δ T - V i 3 α Δ T A ⋅ 1 + 2 α ⋅ Δ T

Colocando V i Δ T :

Δ h = V i Δ T β - 3 α A ⋅ 1 + 2 α ⋅ Δ T

Mandamos bem nessa!!!!!!

Até a próxima questão..............

Resposta

Δ h = V i Δ T β - 3 α A ⋅ 1 + 2 α ⋅ Δ T

Ver Outros Exercícios desse livro