Uma massa de repousa sobre outra massa de que, por sua vez, repousa sobre uma superfície horizontal, como mostra a Fig.. A força varia com o tempo (medido em segundos), de modo que . Se, entre todas as superfícies, o coeficiente de atrito estático é e o coeficiente de atrito cinético é , determine o movimento de cada bloco em função do tempo.
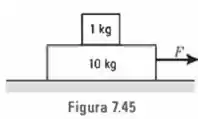
Passo 1
E aí, beleza?? Vamos começar calculando a força máxima que permite que os blocos não deslizem entre si. Para isso, vem:
Assim, para o bloco menor:
Assim:
E o tempo que leva para que a força tenha esse valor é:
Passo 2
Assim, para , os blocos caminham juntos. A velocidade deles é:
Portanto, a posição dos dois blocos em função do tempo é:
Passo 3
Para , sendo a aceleração do bloco menor e a aceleração do bloco maior, vem:
Portanto, as velocidades a partir de (quando a velocidade vale ), sendo a velocidade do bloco menor e a do maior:
E a posição, passa a ser:
Resposta
Ei, a resposta está no passo a passo :)