O momento de dipolo magnético da Terra tem módulo de .

1. Qual a intensidade de campo magnético sobre a superfície da Terra, no polo norte magnético? Como este valor se compara ao valor encontrado na Tabela 33.1? Você pode supor que a espira de corrente esteja dentro da Terra.
2. Os astronautas descobrem um planeta parecido com a Terra e desprovido de um campo magnético. Para criar um campo magnético, de modo que uma bússola funcione, eles propõem fazer fluir uma corrente em um fio ao longo do equador. Que intensidade de corrente seria necessária?

Faaaaaala, galera... Tranquileba??

Precisamos definir primeiro a equação do dipolo magnético. Assim, achemos o campo magnético em função de seu dipolo. Cola comigo!

Seja uma espira ideal:

Então:

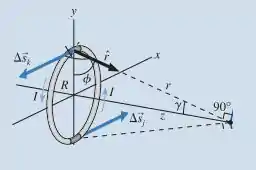
Vemos que as componentes em x e y se cancelam, sobrando somente em z.

Sabendo que a lei de bio-savart é:

Veja que:

Assim:

E que:

E também:

Assim ficando:

Integrando sobre toda a espira:

Concluímos que o campo magnético sobre uma espira é:

Tomando à parte:

Tomando a aproximação de que

Assim, tomando o campo magnético na espira para :

Multiplicando por em cima e em baixo:

Sabemos que

E é chamado de momento de dipolo magnético . Assim:

E a tabela 33.1 citada é:

Com esse “insight” nem precisa mais de mim, né?! Mas se gosta de mim, cola pro próximo passo!