No momento em que um sinal luminoso fica verde, um carro que estava parado começa a mover-se com aceleração constante de . No mesmo instante, um caminhão que se
desloca com velocidade constante de ultrapassa o carro.
a) Qual a distância percorrida a partir do sinal para que o carro ultrapasse o caminhão?
b) Qual é a velocidade do carro no momento em que ultrapassa o caminhão?
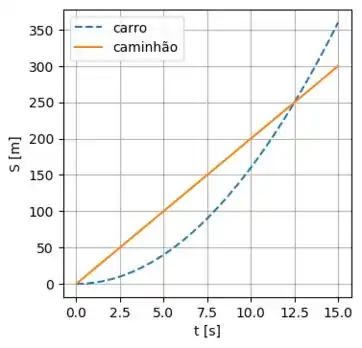
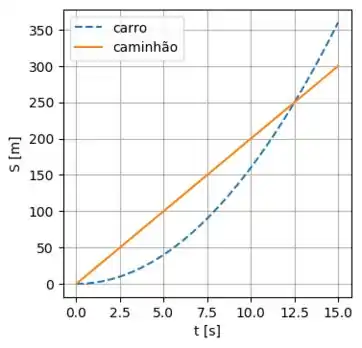
c) Faça um gráfico xt dos movimentos desses dois veículos. Considere o ponto
de intersecção inicial.
d) Faça um gráfico dos movimentos desses dois veículos.
Passo 1
Opa, bora resolver esse problema! Temos a seguinte situação:
O semáforo abre e no mesmo instante: um carro começa a se mover com aceleração e um caminhão a ultrapassa o este carro.
Queremos saber, na letra (A) qual a distância após o sinal que o carro percorre antes de ultrapassar o caminhão.
Bom, pessoal. Primeiro, vamos aplicar a equação do espaço percorrido do movimento uniformemente variado para ambos os veículos.
Para calcular a posição do caminhão, temos os seguintes dados:
Então,
Para calcular a posição do carro, temos os seguintes dados:
Então,
Sabemos que o caminhão começas a ultrapassar o carro a partir do momento que eles estão na mesma posição e no mesmo intante de tempo.
Pois bem, para isso basta igualar a posição do carro e a posição do caminhão que encontramos:
(Vamos arrumar um pouquinho, e tirar as unidades para ficar mais visual, mas não podemos esquece-las depois, ok?)
Passo 2
Assim, podemos encontrar o tempo, , que ainda não sabemos utilizando Bhaskara:
Passo 3
- Agora que encontramos o tempo, o substituímos na relação que encontramos:
- Para sabemos com qual velocidade o carro ultrapassa o caminhão, vamos aplicar a equação de velocidade do movimento uniformemente variado:
- Ambos saem do mesmo ponto, mas como o caminhão tem velocidade constante, representada pela linha laranja, enquanto o carro varia sua velocidae, na linha tracejada, eles voltam a se encontrar no instante
- Aqui, temos que, quando o carro ultrapassa o caminhão, sua velocidade é duas vezes maior que a do caminhão:
Passo 4
Passo 5
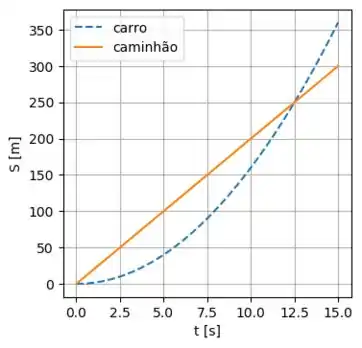
Passo 6
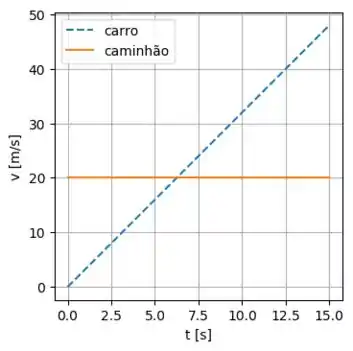
Resposta