Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 9.4 - Ex. 34
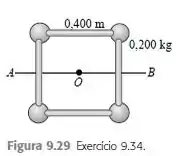
Quatro pequenas esferas, todas consideradas massas puntiformes com massa de , estão dispostas nos vértices de um quadrado de lado igual a e conectadas por hastes leves (Figura ). Calcule o momento de inércia do sistema em relação a um eixo:
a) Perpendicular ao quadrado e passando pelo seu centro (um eixo passando pelo ponto na figura);
b) Cortando ao meio dois lados opostos do quadrado (um eixo ao longo da linha indicada na figura);
c) Passando pelo centro da esfera superior da esquerda e pelo centro da esfera inferior da direita e através do ponto .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o momento de inércia do sistema em relação a um eixo para diferentes configurações.
Nós sabemos que o momento de inércia de um corpo de massa que está a uma distância do eixo de rotação é dado por:
Como temos quatro massas iguais, precisamos apenas determinar a distância de cada uma ao eixo e somar os quatro momentos de inércia. Caso o eixo esteja em cima de uma das massas, ela não contabiliza para o momento de inércia, já que a distância dela até o eixo seria zero =D.
Beleza? Vamos começar?
Passo 2
Letra a)
Para a primeira configuração, temos que o eixo de rotação passa pelo centro do quadrado. Já que as quatro massas estão nos vértices, a distância delas até o eixo é igual para todas e vale metade da diagonal do quadrado, olha só:
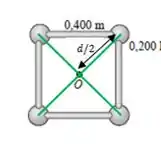
O lado do quadrado é , e a diagonal em função do lado é:
Então a metade da diagonal (que é nossa distância ) é:
Substituindo , temos:
Passo 3
Agora que sabemos a distância até o eixo de cada massa, podemos calcular o momento de inércia desse conjunto. As quatro massas contribuem, então o momento de inércia é a soma dos momentos de inércia de cada uma, ou seja:
Todas as massas são iguais e valem . A distância também é igual e vale . Agora é só substituir:
Tranquilo? A ideia para resolver as outras configurações é a mesma: identificar a distância de cada massa ao eixo e somar todos os momentos de inércia. Vamos pra próxima configuração?
Passo 4
Letra b)
Agora temos que o eixo passa através da linha do desenho. Como o eixo não passa por nenhuma das massas, as quatro vão contribuir novamente para o momento de inércia total. Agora vamos fazer um desenho para ver qual é a distância de cada massa ao eixo:
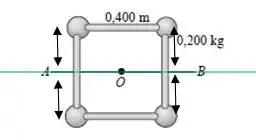
Aqui pode surgir uma dúvida: qual é a distância até o eixo que eu uso? Eu respondo pra você: é sempre a menor! Nesse caso, todas as distâncias são novamente iguais, mas agora valem metade do lado. Como o lado do quadrado é:
A distância será:
Passo 5
Então podemos calcular o momento de inércia total:
Como novamente todas as cargas tem o mesmo peso e a distância é a mesma para o eixo igual a :
Beleza? Vamos pra última configuração?
Passo 6
Letra c)
Pra essa última configuração o eixo passa por duas das massas, então essas duas não vão contribuir para o cálculo do momento de inércia total.
Vou desenhar o eixo em verde pra você ver melhor quais massas entram para o cálculo. O eixo passa no vértice superior esquerdo, centro e vértice inferior direito:
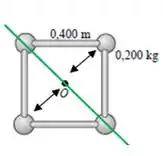
Viu como apenas as duas outras massas vão contribuir? A massa do canto superior direito e inferior esquerdo. E a distância até o eixo? Bom, ela vai ser metade da diagonal, como indiquei com as setas no desenho =)
O valor já conhecemos do passo e vale:
As massas possuem massas iguais e valem , mas atenção, são só duas que vão contribuir! As massas que estão sobre o eixo não somam para o cálculo do momento de inércia!
Passo 7
Então agora é só calcular! Vamos lá?
Como as massas e as distâncias são iguais, temos:
Beleza? Espero ter ajudado!
Valeu, galera! Até a próxima! 😉