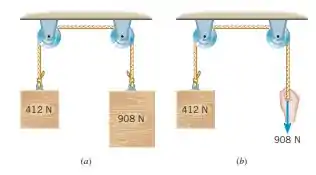
Como mostrado na figura (a), dois blocos são conectados por uma corda que passa por uma polia. Um bloco tem massa 412 N e outro 908 N. A corda e as polias tem massas desprezíveis e não há atrito. (a) Qual é a aceleração do bloco mais leve? (b) Suponha que o bloco mais pesado seja removido e uma força de 908 N seja aplicada como mostrada no desenho (b). Encontre a aceleração do bloco remanescente. (c) Explique porquê as respostas de (a) e (b) são diferentes.
Passo 1
De acordo com a equação 4,5, a massa de cada bloco é dada por:
Passo 2
A tensão na corda pode ser calculada ao fazermos um balanço de forças tal que:
Note que na segunda equação temos um sinal negativo, uma vez que estamos falando do bloco mais pesado e ele desce!!!
(a)
Portanto:
Passo 3
(b) A tensão na corda agora é de 908 N, temos então que:
(c) No primeiro caso, a inércia de AMBOS os blocos afetam a aceleração, enquanto no segundo caso, apenas a inércia do bloco mais leve permanece.
Resposta
Ei, a resposta está no passo a passo :)