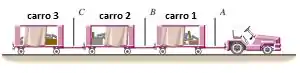
Em um aeroporto, bagagem é descarregado a partir de um plano em três carros de bagagem como mostrado abaixo. A aceleração desse carregamento é de 0,12 m/s², e o atrito pode ser negligenciado. As barras que ligam uma seção a outra tem massa desprezível. O quanto deve ter a tensão em cada barra de ligação A, B e C mudada se 39 kg de bagagem forem removidas do carro 2 e posta no carro (a) 1 e (b) 3? Se a tensão muda, especifique onde ela irá crescer ou diminuir.
Passo 1
E aí gente, tudo bem? A tensão em cada cabo é responsável pela aceleração do objeto atrás do mesmo. As massas dos carros vamos chamar de m1, m2 e m3. Nós podemos usar a segunda lei de Newton para expressar a tensão de cada cabo, considerando o atrito desprezível.
Podemos agora escrever isso considerando variações, se liga!
Passo 2
(a) Movendo a bagagem do carro 2 para o 1, note que não haverá mudança da massa total do sistema, ou seja, e com isso
A transferência do carro 2 para 1 causa uma massa total decrescer para 39 kg, então
A transferência do carro 2 para o carro 1 não muda a massa e, portanto, temos que
Passo 3
(b) Movendo a bagagem do carro 2 para 3 não há mudança de massa total, logo a variação de massa de massa e tensão serão zero no cabo A.
Agora, se transferirmos do carro 2 para o carro 3, note que também não haverá mudança de massa total e por isso, tanto a variação de massa quanto a tensão B serão nulas.
Transferindo do carro 2 para o carro 3, a massa aumenta em 39 kg, então
Resposta
Ei, a resposta está no passo a passo :)