Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Eisberg e Resnick - Física quântica- Ed: 1º - Capítulo 14.Problemas - Ex. 13

A – Mostre que o calor específico a campo constante c H para um sistema de dois níveis, discutido em conexão com (14-5), é dado por

c H = N k 2 μ B k T 2 e 2 μ B / k T e 2 μ B k t + 1 2

Onde N é o número de átomos do sistema. Este é o calor específico de Schottky (Sugestão: Tome como zero a energia dos dipolos alinhados na direção do campo.)

B – Qual é a dependência em temperatura de c H a temperaturas altas e baixas?

C – Faça um esboço de c H em função de T. Estimes (sem calcular) para que temperatura c H será máximo.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!

A - A energia potencial de orientação de dipolos magnéticos com momento μ alinhado paralelamente a um campo magnético B é - μ B e a energia dos dipolos alinhados antiparalelos a B é + μ B , então a diferença entre as duas energias é dada por

Δ E = + μ B - - μ B = 2 μ B

Defina a energia potencial dos dipolos alinhados paralelamente com B para ser zero, de modo que apenas os dipolos alinhados antiparalelos contribuam para a energia potencial do sistema, com uma energia Δ E por dipolo, uma vez que os dipolos paralelos e antiparalelos devem ser separados em energia por este montante.

Calculando a energia potencial U de um sistema multiplicando Δ E pelo número de dipolos alinhados antiparalelos, dado pelo produto de sua densidade numérica n + e o volume V do sistema, nós temos então:

U = n + V Δ E = n + V 2 μ B

Aqui, n + é dado por:

n + = c n e - μ B / k T

Nesta definição, n é o número de momentos dipolares magnéticos desemparelhados por unidade de volume, T é a temperatura, k é a constante de Boltzmann e c é uma constante de proporcionalidade, fazendo a substituição, nós temos

U = c n e - μ B / k T V 2 μ B

Passo 2

A densidade numérica de momentos dipolares magnéticos desemparelhados n também é definida como a soma do número por unidade de volume n - de momentos alinhados paralelamente ao campo e o número por unidade de volume n + de momentos alinhados antiparalelo ao campo

n = n - + n +

Substituindo os valores para os termos de n, obtemos o seguinte resultado

n = c n e μ B / k T + c n e - μ B / k T = c n e μ B k T + e - μ B k T

Isolando a constante c, nós temos que

c = 1 e μ B / k T + e - μ B / k T

Voltando para a energia potencial U e fazendo as devidas substituições, nós temos que

U + = 2 n V μ B e - μ B / k T e μ B / k T + e - μ B / k T  

Simplificando os termos iguais, obtemos que

U + = 2 n V μ B 1 e 2 μ B k T + 1

Defina o produto da densidade numérica de dipolos desemparelhados n e o volume V como o número de átomos N , e substituindo N para n V em U, nós temos que

U = 2 N μ B   1 e 2 μ B k T + 1

Passo 3

O calor específico é definido como a derivada da energia em relação à temperatura

c = ∂ U ∂ T

Faça a derivada da energia potencial calculada em relação a T para obter o calor específico de Schottky c H

c H = ∂ ∂ T   2 N μ B   1 e 2 μ B k T + 1

Com isso, nós obtemos a seguinte derivada

c H = 2 N μ B - 2 μ B k T 2 e 2 μ B k T - 1 e 2 μ B k T + 1 2

Desenvolvendo a derivada, nós temos

c H = N 2 2 μ 2 B 2 k T 2 e 2 μ B k T e 2 μ B k T + 1 2 = N k 2 μ B k T 2 e 2 μ B k T e 2 μ B k T + 1 2

Portanto, o calor específico de Schottky é igual a

c H =   N k 2 μ B k T 2 e 2 μ B k T e 2 μ B k T + 1 2

Passo 4

B – Em altas temperaturas T → ∞ , o fator 2 μ B / k T vai para zero desde que o termo T esteja no denominador, com isso os termos exponenciais tendem a 1 e a dependência de temperatura de c H vai para

c H ≈ N k 2 μ B k T 2 ( 1 ) 1 + 1 2

Com isso, o termo vai para

c H ≈ N k 2 2 μ B k T 2

Portanto, em altas temperaturas, c H depende das temperaturas na ordem de T - 2 , com isso, c H ∝ T - 2 .

Já em baixas temperaturas ( T → 0 ) , o fator 2 μ B k T vai para infinito, como 2 μ B k T → ∞ , os termos exponenciais rapidamente se aproximam do infinito, o denominador é “denominado” pelo termo exponencial, logo

c H ≈ N k 2 μ B k T 2 e 2 μ B / k T e 2 μ B k T 2

Que passa a ser

c H ≈ N k 2 μ B k T 2 e - 2 μ B k T

Portanto, em baixas temperaturas, c H   depende da temperatura na ordem de c H ∝ T - 2 e - 2 μ B / k T .

Passo 5

C – Definindo uma variável adimensional x, temos que

x = 2 μ B k T

Substituindo esse x em c H , nós temos:

c H = N k x 2 e x e x + 1 2

Dividindo o c H por N k , para deixar tudo adimensional, obtemos o seguinte resultado

c H N k = x 2 e x e x + 1 2

Fazendo o gráfico de c H N k como uma função de x:

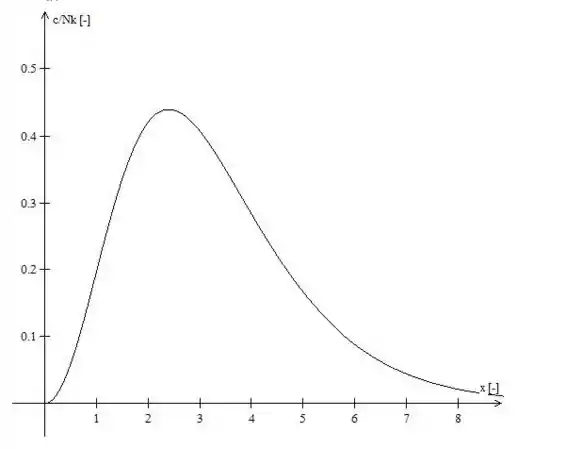
inspecione o gráfico de c H para descobrir que ele tem um máximo quando o parâmetro adimensional x tem um valor de cerca de 2,5. Colocando 2 μ B / k T como 2,5 e resolvendo para μ B temos que

2 μ B k T = 2,5  

Logo, temos que

μ B = 2,5 2 k T = 1,25   k T

Portanto, c H é um máximo quando o potencial de energia do dipolo e as características termais de energia satisfazem μ B = 1,25   k T .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro