Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 5.Problemas - Ex. 75

Mostre que as componentes da aceleração, segundo os vetores unitários u → r e u → θ (Fig. 5.26), são

a r = d 2 r d t 2 - r d θ d t 2 , a θ = 2 d r d t d θ d t + r d 2 θ d t 2

[Sugestão: usar a expressão (5.63) para a velocidade e levar em conta os valores de d u r / d t e d u θ / d t ]

Passo 1

Opaa tudo bem?

Vamos lá para mais um problema bem legal ein!

A figura 5.26 é a seguinte

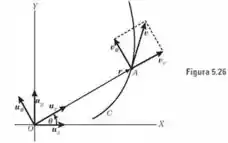
Passo 2

Na Seção 5.11 do livro, o autor diz que

u → θ = - u → x sin ⁡ θ + u → y cos ⁡ θ

u → r = u → x cos ⁡ θ + u → y sin ⁡ θ

E para a velocidade:

v r = d r d t

v θ = r d θ d t = ω r

Passo 3

A expressão 5.63 é a seguinte

v = u → r d r d t + u → θ r d θ d t

Passo 4

Para a aceleração, devemos derivar a expressão para a velocidade em relação ao tempo

a = d v d t = u r d 2 r d t 2 + d r d t d u r d t + u θ r d 2 θ d t 2 + u θ d r d t d θ d t + r d u θ d t d θ d t

E temos que

d u r d t = u θ d θ d t

d u θ d t = - u r d θ d t

Então, para a aceleração temos que

a = u r d 2 r d t 2 + r d s d t 2 + u θ r d 2 θ d t 2 + 2 d r d t d θ d t

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro