Urna roda de raio R rola com velocidade constante ao longo de um plano horizontal. Prove que a posição de qualquer ponto em sua periferia é dada pelas equações x = R(wt - sen wt) e y = R (1 - cos wt), onde w = v/R é a velocidade angular da roda e t é o tempo medido desde o instante em que o ponto está em contato com o plano. Obtenha as componentes ela velocidade e da aceleração elo ponto

Vou fazer um desenho esquemático pra ficar mais fácil de a gente observar, beleza?

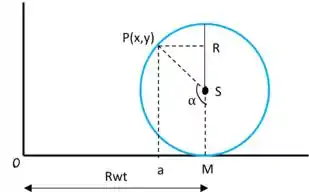
Em , . O ângulo varrido por é

Suponhamos que não há deslizamento, então a distância percorrida é igual ao diâmetro

O ângulo é definido como

Vamos achar as coordenadas do ponto

Onde

Para

Onde

Agora, para velocidade nas direções temos

Para a aceleração temos que