Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 41.Problemas adicionais - Ex. 45

  1. Mostre que a derivada d P / d E da Eq. 41-6 é - 1 / 4 k T para E = E F . (b) Mostre que a tangente à curva da Fig.41-7b no ponto E = E F intercepta o eixo horizontal no ponto E = E F + 2 k T .

Passo 1

Aparentemente temos um problema mais matemático do que físico. Vamos recordar que

P E = 1 e E - E F k T + 1

Passo 2

  1. No primeiro item, temos que calcular a derivada de P E em relação a Energia, ou seja

    2. d P d E =   - e E - E F k T k T e E - E F k T + 1 2

    Para E = E F temos e E - E F k T → 1 , assim

    d P d E = 1 k T 2 2 = 1 4 k T

    Passo 3

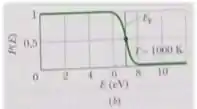
  2. A Fig. 41-7b é

Temos do item (a) que a derivada de P E em função da energia é a reta tangente do nosso problema também.

Desta forma podemos escrever que a reta pode ser escrita como

y = α x + c o n s t a n t e = - 1 4 k T E - E 0 = P ( E )

Em E = E F → P E F = 1 / 2  

1 2 = 1 4 k T E F - E 0 → E 0 = E F - 2 k T

O que mostra que em E = E F nossa reta é tangente a reta E = E F - 2 k T

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro