Um número infinito de cargas positivas e negativas + -q são arranjadas alternadamente em uma linha reta. O espaçamento entre as cargas adjacentes é o mesmo e igual, r (Fig. 14-49). Mostre que a energia potencial de uma carga é . [ Dica: Use a Eq. (M. 24).]
Passo 1
Opaaa tudo certo?
Vamos lá para mais um problema bem legal ein! A figura dada no problema é a seguinte
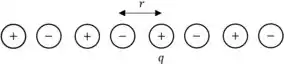
Passo 2
O potencial pode ser calculado por
Passo 3
A expansão de Taylor para o logaritmo natural é
Para
Passo 4
Podemos simplificar a relação para o potencial
Passo 5
Logo a energia potencial será
Resposta
Ei, a resposta está no passo a passo :)