Um elétron, após ser acelerado por uma diferença de potencial de 565 V, entra em um campo elétrico uniforme de 3500 Vm em um ângulo de 60 com a direção do campo. Após 5x10 ^ -8. Quais são (a) os componentes de sua velocidade paralela e perpendicular ao campo, (b) a magnitude e a direção de sua velocidade, (c) suas coordenadas em relação ao ponto de entrada? (d) Qual é a sua energia total?

a. Vamos calcular a velocidade que o eléctron tem depois de ser acelerado pela diferença de potencial

Temos todos os valores necessários

As componentes da velocidade são dadas da seguinte forma

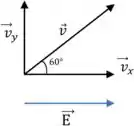
E suas componentes podem ser calculadas como

A velocidade na direção permanecerá constante, já que não tem forças agindo nessa direção. Já a velocidade na direção irá mudar:

E, como em não vai ter mudança

b. O módulo de um vetor é dado por . Resolvendo para a velocidade, temos

A direção de um vetor é dada por . Para o ângulo de direção do vetor velocidade temos

c. O ponto P tem as coordenadas:

d. a Energia é dada por