Um objeto de 2,0 cm de altura encontra-se 15 cm à frente de uma lente divergente cuja distância focal vale -20 cm.
a. Use o traçado de raios para determinar a posição e a altura da imagem. Para efetuar isso com precisão, use uma régua ou um papel quadriculado. Determine a distância da imagem e a altura da mesma efetuando medições em seu diagrama.
b. Calcule a posição e a altura da imagem. Compare com suas respostas obtidas pelo traçado de raios do item anterior.
Passo 1
De novo! Bom! Ctrl C + Ctrl V, hehehe
a.
Traçando os raios particulares chega-se numa figura como esta:
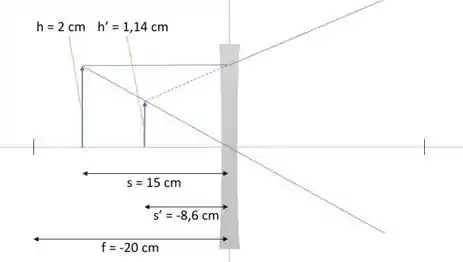
Para esse simples objeto, traçar dois raios é suficiente para encontrar a posição da imagem. E por esse método, obtém-se para a imagem posição e altura .
Passo 2
b.
Matematicamente, pela equação da lente delgada pode-se calcular a posição da imagem do objeto, que está na posição , conjugada por uma lente de distância focal :
Sabendo-se que a altura do objeto é , pela relação de proporcionalidade entre posição e altura, a altura da imagem pode ser encontrada:
Esses resultados conferem com os resultados obtidos por meio dos traçados.
Suave, né? Hehe
Resposta
b. 8,6 cm; 1,14 cm.