Um objeto de 2,0 cm de altura encontra-se 20 cm à esquerda de uma lente com distância focal de 10 cm. Uma segunda lente, com distância focal de 5 cm, encontra-se 30 cm à direita da primeira lente.
a. Use o método de traçado de raios para determinar a posição e a altura da imagem. Faça isso com precisão, usando uma régua ou papel quadriculado. Estime a distância da imagem e a altura da mesma efetuando medições em seu diagrama.
b. Calcule a posição e a altura da imagem. Compare com suas respostas obtidas do traçado de raios no item anterior.
Passo 1
Fala pessoal, tudo belezinha? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Primeiramente, vamos anotar as variáveis, para se situar na questão
Para a letra a), basta fazer o diagrama, que esse aqui:
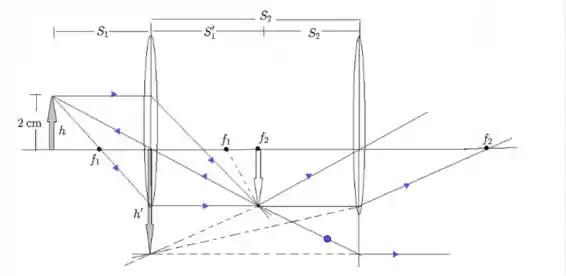
Passo 2
Para a letra b) nós temos que encontrar , para isso vamos usar a equação da lente fina:
Manipulando a equação, vai ser dado por:
Agora, vamos substituir os valores:
A ampliação para a primeira lente é dada da seguinte forma:
Passo 3
Para encontrar a segunda lente, temos que usar de novo a equação da lente fina, com isso, temos:
Manipulando a equação, temos o valor de
A ampliação da segunda lente é dada por:
A ampliação total é dada pela soma das duas ampliações: