Um objeto de 2,0 cm de altura é posicionado na frente de um espelho. Uma imagem direita de 1,0 cm de altura é formada atrás do espelho, a 150 cm do objeto. Qual é a distância focal do espelho?
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Primeiro vamos anotar as variáveis
A imagem é vertical e forma-se atrás do espelho, ficando como essa imagem aqui
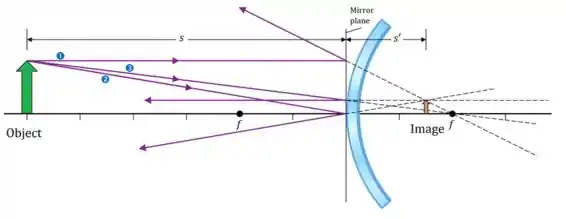
A questão nos pede a distância focal de espelho, e vamos encontrar! 😊
Passo 2
A magnitude da ampliação é encontrada em termos das alturas do objeto e da imagem pela equação
Substituindo os valores numéricos, nós temos
O sinal de M é positivo uma vez que a imagem está na vertical. Partindo para a outra equação, temos que a magnitude do espelho é dada por termos do objeto e distância da imagem, com isso, temos a seguinte relação
Substituindo os valores, obtemos o seguinte resultado
Isolando o s’
Observe que ainda estamos dependendo de termos variáveis, mas logo vamos resolver isso
Passo 3
A distância entre o objeto e a imagem é igual a soma da distância do objeto até a lente e a distância da imagem, com isso, nós temos
Substituindo o para o termo , obtemos
Entenda que o sinal será positivo por causa do módulo
Portanto, como , temos que
Agora, é usar a equação de lente fina
Rearranjando e isolando o , temos que
Substituindo os valores numéricos, nós temos
O sinal negativo indica que o espelho é convexo (assim como no gráfico)