Um objeto de 1,0 cm de altura encontra-se 60 cm à frente de uma lente divergente com distância focal de 30 cm.
Use o método de traçado de raios para determinar a posição e a altura da imagem. Para realizar isso com precisão, use uma régua ou um papel quadriculado. Determine a distância da imagem e a altura da mesma efetuando medições em seu diagrama.
b. Calcule a posição e a altura da imagem. Compare com suas respostas obtidas pelo traçado de raios do item anterior.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!!
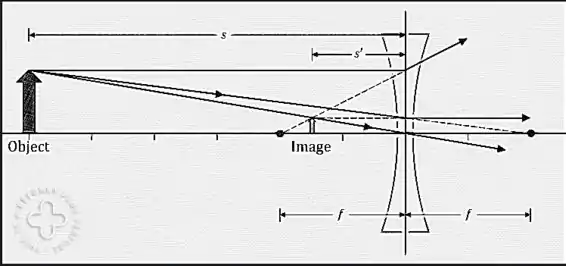
Primeiramente, para localizar a imagem de uma lente divergente, os três raios serão desenhados no topo do objeto. Partindo para uma modelagem, temos que o raio 1 é desenhado paralelo ao eixo principal, para logo, ser refratado pela lente, e portanto, esse raio irá emergir direcionado para longe do ponto focal (isso na parte frontal da lente).
O raio 2 é desenhado na direção do ponto focal na parte posterior, e irá emergir da lente de modo paralelo ao eixo principal, já o raio 3 é desenhado através do centro da lente e continua em linha reta.
Basicamente nós iremos utilizar a equação de lente fina e a ampliação da lente, com isso, temos que a imagem a ser idealizada e pensada para resolver é igual a essa aqui.
Antes de começar a resolver a letra a, vamos anotar as variáveis dadas pelo enunciado, então temos que
Passo 2
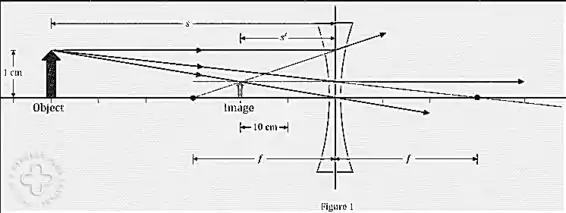
A – Na letra a), nós queremos determinar a distância da imagem h, o eixo óptico é apresentado por uma escala (dado a imagem apresentada no passo anterior), com isso, a lente desenhada e os pontos focais são marcados. Com isso, os raios divergem da lente, mas podemos usar uma regra de três para fazer uma extensão até o ponto em que os raios divergem, logo, esse é o ponto da imagem. Na imagem, o termo ‘s’ é igual a (esse sinal negativo indica que a imagem é virtual), e como o h’ = 0,33 cm, temos que
Passo 3
B – Na letra b), precisamos calcular as mesmas situações, só que agora é de maneira analítica, e com isso, fazer comparações, então, vamos lá
Primeiro, vamos utilizar a equação de lente fina, que é dada da seguinte forma
Isolando o , temos que
Agora, isolando o s’, obtemos o seguinte resultado
Substituindo pelos valores numéricos, temos
A ampliação lateral da lente é encontrada em termos do objeto e distâncias da imagem de
Substituindo pelos valores numéricos
A magnitude (ou seja, o módulo) é encontrado pelo tamanho das imagens vistas pelo objeto
Isolando o h’, temos que
Mais uma vez, substituindo os valores numéricos, nós temos que
Esses valores são exatamente iguais aos da letra a)