Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.3 - Ex. 32
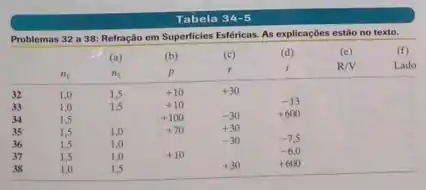
Um objeto O está sobre o eixo central de uma superfície refratora esférica. Para cada problema, a Tabela 34-5 mostra o índice de refração do meio em que se encontra o objeto, o índice de refração do outro lado da superfície refratora, a distância do objeto p, o raio de curvatura da superfície e a distancia da imagem . Determine os dados que faltam, incluindo se a imagem é real ou virtual e se a imagem fica do mesmo lado da superfície que o objeto ou do lado oposto .
Passo 1
Como a gente pode ver na tabela, as letras (a), (b) e (c), já foram respondidas. (d) Vamos então encontrar a distância da imagem formada pela superfície. Para isso, vamos usar a equação de superfícies refratoras esféricas, já que temos tudo que precisamos dado pela tabela:
Então isolamos :
E substituímos os valores de cada letra:
Passo 2
(e) Podemos ver pelo Passo anterior que, , então a imagem vai ser virtual .
Passo 3
(f) Sempre que a imagem for virtual no caso de uma superfície esférica ela será formada do mesmo lado da superfície .