Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 20

Sem fazer a aproximação paraxial, calcule a distância q da “imagem” produzida por uma superfície refratora esférica convexa de raio de curvatura R para um raio incidente paralelo ao eixo, em função do índice de refração relativo n 12 e do ângulo de incidência θ 1 . Mostre que o resultado depende de θ 1 , mas, na aproximação paraxial, reduz-se à distância focal imagem, independente de θ 1 .

Passo 1

O exercício pede para deduzirmos a equação para a posição da imagem produzida por uma superfície refratora esférica de raio R para um raio que incide paralelo ao eixo com ângulo de incidência θ 1 . A figura a seguir ilustra a situação:

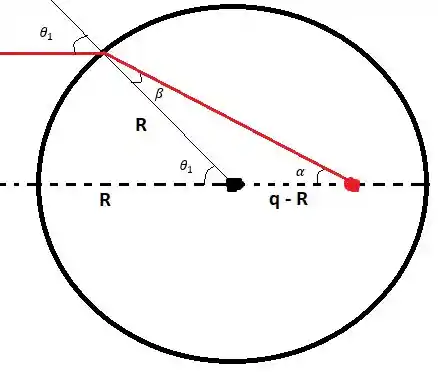
Note que não devemos fazer a aproximação paraxial. O primeiro passo é considerar a refração quando o raio incide sobre a esfera:

n 1   s e n   θ 1 = n 2   s e n   β ⇒ s e n   β = n 1 n 2   s e n   θ 1

Definindo o índice de refração relativo como

n = n 2 n 1 ⇒ s e n   β = s e n   θ 1 n

Vamos guardar essa equação.

Passo 2

Aplicando a lei dos senos no triângulo com ângulos β e α :

q - R s e n   β = R s e n   α

Portanto,

q - R = R   s e n   β s e n   α ⇒ q = R 1 + s e n   β s e n   α

Mas note também que

θ 1 = α + β ⇒ α = θ 1 - β

Logo,

s e n   α = s e n   θ 1 - β = s e n   θ 1 cos ⁡ β - s e n   β cos ⁡ θ 1

Já sabemos que

s e n   β = s e n   θ 1 n

Logo, como cos 2 ⁡ β + s e n 2   β = 1 :

cos ⁡ β = 1 - s e n 2 β = 1 - s e n 2   θ 1 n 2

Portanto,

s e n   α = s e n   θ 1 1 - s e n 2   θ 1 n 2 - s e n   θ 1 n ⋅ cos ⁡ θ 1 = s e n   θ 1 n n 2 - s e n 2 θ 1 - cos ⁡ θ 1

Passo 3

Com isso,

q = R 1 + s e n   β s e n   α = R   1 + s e n   θ 1 n s e n   θ 1 n n 2 - s e n 2 θ 1 - cos ⁡ θ 1

Logo,

q = R   1 + 1 n 2 - s e n 2 θ 1 - cos ⁡ θ 1

Essa é a expressão pedida! Agora vamos tomar o limite paraxial com θ 1 → 0 :

s e n   θ 1 → 0               e         cos ⁡ θ 1 → 1

Assim,

q → R   1 + 1 n - 1 = R n n - 1

Ou ainda,

1 q → 1 R n - 1 n = 1 R 1 - 1 n 2 / n 1 = 1 R 1 - n 1 n 2 = 1 R n 2 - n 1 n 2 = 1 f

Vemos que no limite paraxial, a imagem é formada no foco!

Resposta

q = R   1 + 1 n 2 - s e n 2 θ 1 - cos ⁡ θ 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Exercício 34.20 supondo que a extremidade esquerda do bastão seja uma superfície hemisférica côncava com raio igual a 4,0 cm.20) A extremidade esquerda de um longo bastão de vidro com diâmetr
Uma camada de 2,00 cm de espessura de água(n1=1,33) flutua sobre uma camada de 4,00 cm de espessura de tetracloreto de carbono(n=1,46)em um tanque.A que distancia abaixo da superficie superior da agua
RICO EM CONTEXTO Durante as ferias,voce esta merguIhando e usando uma mascara de mergulho que tem um bojo saliente para fora,com um raio de curvatura de 0,50 m.Como consequencia, existe uma superficie