Obtenha a lei do deslocamento de Wien, , resolvendo a equação .
Sugestão: faça e mostre que a equação citada leva a . Mostre então que é solução.
Passo 1
Fala galerinha, beleza?
Queremos encontrar o valor de que maximiza a curva espectral . Para isso, temos que lembrar que
Além disso, aconselho você dar uma olhadinha no problema 12 em que eu demonstro que
Assim,
Temos que derivar essa expressão com relação a e igualar a .
Passo 2
Tomando a derivada:
Assim,
Daí, tiramos que
Seguindo a sugestão do enunciado, fazemos a substituição :
Logo,
Dividindo a equação por :
Essa é a equação que enunciado disse que chegaríamos e cuja solução é . Se trata de uma equação transcendental e a única forma de resolvê-la é numericamente. Uma boa forma é plotar as funções e e localizar o ponto de encontro:
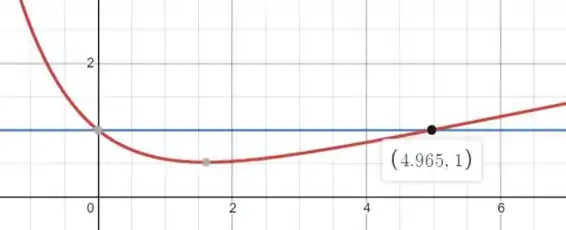
Feito isso, temos que
Chamando esse de , achamos
Essa é a lei do deslocamento de Wien:
Resposta
Demonstração.