Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Eisberg e Resnick - Física quântica- Ed: 1º - Capítulo 2.Problemas - Ex. 14

Obtenha a relação

cot ⁡ θ 2 = 1 + h v m 0 c 2 tan ⁡ ϕ

Entre as direções de movimento do fóton espalhado e do elétron envolvidos no efeito Compton.

Passo 1

E aí, beleza? Nessa questão, iremos utilizar a equação do espalhamento Compton e também a conservação do momento. O esquema do problema é o seguinte:

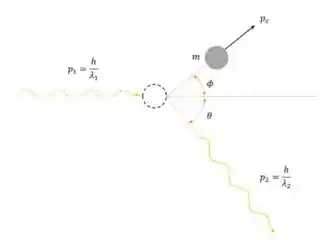
Passo 2

Vamos conservar primeiramente o momento na vertical e na horizontal. Vamos escrever o momento em função da frequência da onda, em vez do seu comprimento de onda, assim, vem:

Na horizontal:

h v c = h v 2 c cos ⁡ ( θ ) + p e cos ⁡ ( ϕ )

Na vertical:

p e sen ⁡ ( ϕ ) = h v 2 c sen ⁡ ( θ )

Assim, note que, a cotangente de ϕ é dada por:

cot ⁡ ( ϕ ) = v - v 2 cos ⁡ ( θ ) v 2 sen ⁡ ( θ ) = v v 2 - cos ⁡ ( θ ) s e n ⁡ ( θ )

Passo 3

Da equação do espalhamento Compton, temos:

c v 2 = c v + h m 0 c   1 - cos ⁡ θ  

Portanto:

v v 2 = 1 + h v m 0 c 2   1 - cos ⁡ θ

Passo 4

Das duas equações, temos:

cot ⁡ ( ϕ ) = 1 + h v m 0 c 2   1 - cos ⁡ θ - cos ⁡ ( θ ) sen ⁡ ( θ ) = 1 - cos ⁡ θ sen ⁡ θ 1 + h v m 0 c 2

Da trigonometria, sabemos que:

tan ⁡ θ 2 = 1 - cos ⁡ θ sen ⁡ θ

Portanto:

cot ⁡ ( ϕ ) = tan ⁡ θ 2 1 + h v m 0 c 2

Portanto, invertendo:

cot ⁡ θ 2 = 1 + h v m 0 c 2 tan ⁡ ϕ

Como queríamos demonstrar!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro