Uma onda que se propaga na água é chamada de onda profunda se a profundidade da água for maior do que um quano do comprimento de onda. Diferente das onda~ considerndas neste capículo. a velocidade de uma onda profunda na água depende de seu comprimemo de onda: v=~ Comprimentos de onda maiores se propagam mais rapidamente. Vamos aplicar este fato para ondas estacionárias. Considere uma piscina de mergulho com 5,0 m de profundidade e 10,0 m de Jar: gura. Ondas estacionárias podem ser criadas na água e se propagar no sentido da largura da piscina. Como a água se agita para cima e para baixo nas laterais da piscina, as condições de contorno requerem antinodos cm x = O ex = L. Assim, uma onda estacionária na água se assemelha a uma onda sonora cstacionítria em um tubo aberco-aberto. a. Quais são os comprimentos de onda dos primeiros três modos de onda estacionária para a água da piscina? Eles satisfazem a condição para serem considerados ondas profundas? Desenhe um gráfico para cada um dos modos. b. Quais são as velocidades de onda de cada uma dessas ondas? e. Derive uma expressão geral para as freqüências f.. das possíveis ondas estacionárias. A expressão deve ser uma função de m, de g cdeL. d. Quais são os períodos de oscilação dos três primeiros modos de onda estacionária?
Passo 1
E aiii gente, tudo bom com vocês?
Então vamos resolver essa questão bem legal aqui e passo a passo pra gente tirar 10 na provinha!
Vamo lá!
Letra a:
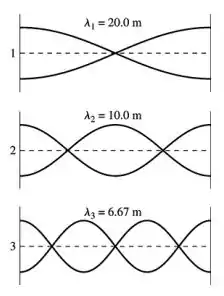
Os comprimentos de onda dos modos de onda estacionária são:
A profundidade da piscina é de 5.0m. Claramente, as ondas estacionárias com e são "ondas de águas profundas" porque a profundidade de 20 m é maior do que um quarto do comprimento de onda. A onda com mal se qualifica para ser uma onda de água profunda parada.
Passo 2
Letra b:
A velocidade da onda para o primeiro modo de onda estacionária é:
Da mesma forma,
Passo 3
Letra c:
Nós temos
Observe que m é o modo e não a massa.
Passo 4
Letra d:
O período de oscilação para o primeiro modo de onda estacionária é calculado da seguinte forma:
Da mesma forma,
Resposta
- Ver desenho
- Ver resposta
- Ver resposta