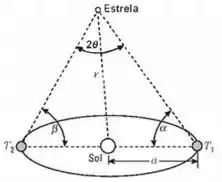
Paralaxe é a diferença na direção aparente de um objeto, resultante ela mudança de posição do observador. (Segure um lápis na sua frente e feche inicialmente o olho direito e depois o esquerdo. Observe que, em cada caso, o lápis parece situado em posição diferente, em relação ao plano de fundo.) Paralaxe estelar é a mudança aparente, da posição de uma estrela, como resultado do movimento orbital da Terra em torno do Sol. Ela é dada, quantitativamente, pela metade do ângulo, subentendido pelo diâmetro da órbita terrestre perpendicular à linha que une a estrela ao Sol (veja Fig. 2.10). Ela é dada por , sendo os ângulos e medidos nas duas posições separadas por seis meses. A distância , da estrela ao Sol, pode ser obtida pela relação , onde é o raio da órbita terrestre e é expresso em radianos. A estrela que apresenta maior paralaxe, cujo valor é (isto é, a estrela mais próxima) é a -Centauro. Calcule a sua distância do Sol, expressa em metros, anos-luz e unidades astronômicas (.).
Passo 1
E aí, beleza?? Essa questão, apesar de parecer complexa, não irá nos exigir muitos cálculos. Nos baseando pela figura do enunciado, para calcular a distância da estrela ao Sol, basta calcular , em que é a distância média da Terra ao Sol que é, por definição, . Assim, precisamos apenas converter o ângulo da paralaxe de segundos para radianos.
Nesse intuito, sabemos que em um minuto, existem segundos, logo:
E, como existem minutos em , vem:
Portando, para converter para radianos, multiplicamos por . Por fim, chegamos em:
Assim, a distância da estrela ao Sol fica:
Passo 2
Convertendo para as outras unidades sugeridas, como já foi feito nos problemas anteriores, chegamos em: