Uma partícula de massa m, inicialmente em repouso, está sujeita a uma força durante o intervalo . Prove que a velocidade da partícula no fim do intervalo é de . Note que ela depende somente do produto e, se decresce, a mesma velocidade é atingida, aumentando-se proporcionalmente. Represente graficamente versus . Você é capaz de imaginar uma situação física para a qual este problema seja uma descrição adequada?
Passo 1
E aí, beleza?? Vamos resolver essa questão por integração direta:
Portanto:
Ou seja:
Por fim:
Como queríamos demonstrar.
Passo 2
O gráfico de por é do tipo:
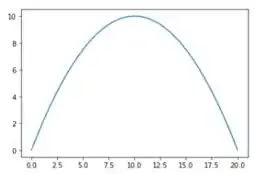
O gráfico foi montado tomando e .
Passo 3
Há uma situação física bem simples que a força se assemelha à dada pelo problema. Imagine uma partícula presa em um aro circular, sendo submetida a uma aceleração tangencial constante. Assim, ela terá velocidade linear do tipo:
E assim, a força exercida pelo aro será a resultante centrípeta, dada por:
Que é uma parábola com concavidade para cima. Porém, perceba que a força exercida pela partícula no aro é:
Que é uma parábola com concavidade negativa, assim como a força do problema, diferindo desta apenas por uma constante inicial.
Resposta
Ei, a resposta está no passo a passo :)