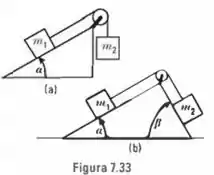
Determine a aceleração com a qual os corpos, na Fig. (a) e (b), movem-se, e também as tensões nos fios. Admita que os corpos deslizam sem atrito. Resolva os problemas de uma maneira geral, inicialmente, e, em seguida, aplique ao caso , , e .
Passo 1
E aí, beleza?? Vamos resolver de maneira genérica, considerando os ângulos e . Escrevendo a segunda lei de Newton para os dois corpos no eixo paralelo ao plano inclinado, temos:
Somando, temos:
Agora para a tração:
Portanto:
Passo 2
Substituindo os valores, vem:
(a)
(b)
Resposta
(a)
(b)