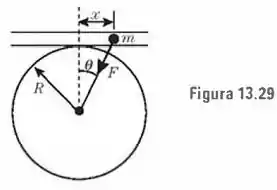
Uma partícula de massa pode se mover num tubo horizontal sem atrito (Fig. 13.29), sob a ação da atração gravitacional da Terra. Supondo que seja muito pequeno, comparado com , demonstre que a partícula executa um movimento harmônico simples e que seu período é . Calcule o valor de . Esse valor corresponde ao período mais longo de um pêndulo na superfície da Terra. Você pode demonstrar essa afirmação?
Passo 1
E aí, beleza?? Vamos calcular a força no eixo horizontal quando a partícula está na posição indicada na figur. Assim, vem:
Ou seja:
Que, em primeira ordem, é dada por:
Passo 2
Da segunda lei de Newton, temos:
Ou seja:
Que é justamente a equação de um MHS em torno de , com período dado por:
Como queríamos demonstrar.
Note que, como o período de um pêndulo é e, como não é possível termos um pêndulo do tamanho do raio da Terra (pelo menos eu acho kkk), esse período que calculamos é o maior possível para um pêndulo.
Passo 3
Numericamente, vem: