Enunciado
Física - Griffiths - Mecânica Quântica- Ed: 2º - Capítulo 2.Problemas - Ex. 7 a
Uma partícula em um poço quadrado infinito tem a função de onda inicial
- Esboce e determine a constante .
Passo 1
Fala aí, beleza? Nesse item vamos fazer uma rápida análise dessa função de onda e então montaremos seu gráfico.
Primeiramente, vamos analisar ela no intervalo .
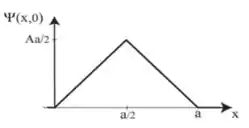
Nesse intervalo, a função de onda é uma reta crescente que passa pela origem, com coeficiente angular , sendo seu valor máximo em , valendo:
Agora, para , temos uma reta decrescente com coeficiente angular , possuindo seu valor máximo também em , valendo:
Perceba que essa função é contínua, como deveria ser! Por fim, perceba também que em , a função de onda se anula:
Ou seja, essa função é a união dessas duas funções gera um triângulo isósceles! Isso ocorre, pois a inclinação, em módulo, das duas partes são iguais, assim como o tamanho delas (ambas com ) no eixo .
Passo 2
Com as informações obtidas no passo anterior, podemos montar o gráfico de , como se segue:
Passo 3
A constante de normalização deve ser tal que:
Portanto, vem:
Abrindo as contas, chegamos em:
Resposta
