No pêndulo da Fig. , a bola descreve uma circunferência horizontal com velocidade angular . Calcule a tensão na corda e o ângulo que ela faz com a vertical para o caso em que , e .
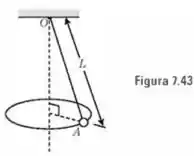
Passo 1
E aí, beleza?? Vamos escrever as equações do movimento (equilíbrio vertical e resultante centrípeta). Seja o ângulo da corda com a vertical, vem:
Então, vem:
Passo 2
Note que a velocidade angular fornecida no enunciado é extremamente alta para a situação (aproximadamente voltas por segundo), o que fará a resposta obtida destoar do gabarito. Porém, provavelmente houve um erro de digitação no enunciado, de modo que a velocidade angular real do problema seja , que é uma velocidade angular mais plausível para o problema. Desse modo, podemos obter o gabarito correto: