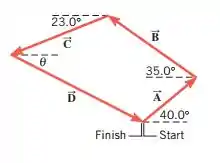
Um percurso de regata de veleiro consiste em quatro pernas, definidas pelos vetores de deslocamento , e , como o desenho indica. As magnitudes dos três primeiros vetores são
, e . A linha de chegada do curso coincide com o início
linha. Usando os dados do desenho, encontre a distância da quarta perna e o ângulo .
Passo 1
Falaaaaaaaaaaaaaaaa Tribuxo?
Bora resolver mais uma questão!?
Uma vez que a linha de chegada é coincidente com a linha de partida, a rede o deslocamento do veleiro é zero. Daí a soma dos componentes do deslocamento os vetores das pernas individuais devem ser zero. No desenho do texto, as instruções para o direita e para cima são considerados positivos.
Para a distância horizontal, teremos:
Passo 2
Para a distância vertical, temos:
Passo 3
Para determinar , dividiremos as duas equações (a segunda pela primeira):
Passo 4
Agora para determinar , faremos:
Foi divertido!!!!
Bora matar mais uma!