Um pinguim desliza a uma velocidade constante de 1,4 m / s para baixo uma inclinação gelada. A inclinação se inclina acima da horizontal em um ângulo de 6,9. Na parte inferior da inclinação, o pinguim desliza para uma área horizontal de gelo. O coeficiente de atrito cinético entre o pinguim e o gelo é o mesmo para a inclinação e para o patch horizontal. Quanto tempo é necessário para que o pinguim pare depois de entrar na horizontal pedaço de gelo?
Passo 1
Oiii tudo certo?
Vamos lá fazer mais um problema bem legal?! Essa é uma questão cheia de truquezinhos, então vamos fazer bem com calma pra não nos perdermos, beleza?
Passo 2
O pinguim para na superfície horizontal porque a força de atrito cinética se opõe ao movimento e faz com que ele desacelere.
O tempo necessário para o pinguim deslizar até parar () após entrar no pedaço de gelo horizontal é
Passo 3
A gente então deve determinar a aceleração do pinguim enquanto ele desliza na horizontal. Fiz um diagrama pra gente entende melhor, se liga:

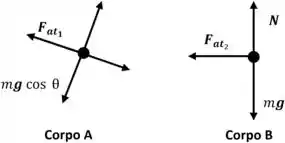
Passo 4
Para o pinguim deslizando no pedaço de gelo horizontal, nós achamos, a partir do diagrama de corpo livre do Corpo B e da segunda lei de Newton na direção (direita positivo) é
Na direção , o diagrama de corpo livre para o Corpo B, temos que
Então, a aceleração do pinguim é
Passo 5
A equação para a aceleração no eixo nos diz que, para acharmos a aceleração , precisamos do coeficiente de atrito cinético .
O enunciado fala pra gente que o coeficiente de atrito cinético entre o pinguim e o gelo são iguais tanto para a inclinação como para a faixa horizontal. Portanto, podemos usar o movimento do pinguim na inclinação para determinar o coeficiente de atrito e usar na equação para .
Para o pinguim deslizando no plano inclinado, achamos o diagrama pro Corpo A e da segunda lei de Newton, temos que
Para a equação anterior, usamos o fato de que o pinguim desliza pela inclinação com uma velocidade constante, de modo que tem aceleração zero.
Sabemos que
Passo 6
Aplicando a segunda lei de Newton na direção perpendicular à inclinação, temos
E, , substituindo isso na equação obtida temos que
Resolvendo para o coeficiente de atrito cinético
Passo 7
Finalmente, o tempo para o pinguim deslizar é dado por