Uma pipa está pairando sobre o solo no final de uma reta Linha de 43 m. A tensão na linha tem magnitude de 16 N. O vento que sopra na pipa exerce uma força de 19 N, direcionada 56 acima da horizontal. Observe que a linha presa à pipa não está orientada em um ângulo de 56 acima da horizontal. Encontre a altura da pipa, em relação à pessoa segurando a linha.

Fiz um desenho esquemático pra ajudar a gente entender melhor o problema beleza?

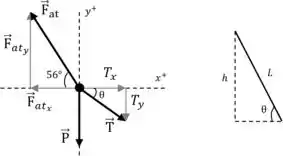
Como a linha da pipa é reta, a distância entre a pipa e a pessoa segurando a linha é , como mostrado na parte direita do desenho.

Como a gente quer encontrar a altura da pipa, precisamos saber o ângulo que a linha da pipa faz com a horizontal. Uma vez que isso seja conhecido, dará a altura da pipa em relação à pessoa.

A dica de chave de ouro para encontrar o ângulo

é a gente saber que a força de tensão exercido na pipa pela linha é paralelo à própria linha. Portanto, a tensão é direcionada a um ângulo abaixo da horizontal.

Para encontrar o ângulo , a gente só precisa encontrar um dos componentes da força de tensão, seja ou , porque a magnitude da tensão é conhecida.

Tanto a força do vento quanto a tensão têm componentes horizontais e verticais, enquanto a força de peso é puramente vertical.

Portanto, existem apenas duas forças horizontais atuando na pipa (, ), mas três forças verticais (, , ), então será mais fácil calcular , o componente horizontal da tensão.

Porque a pipa é estacionária, a componente horizontal da tensão deve equilibrar o componente horizontal da força exercida sobre a pipa pelo vento:

Do diagrama de corpo livre da pipa, podemos ver que os componentes do eixo da tensão e da resistência do ar são e .

Substituindo essas relações na igualdade obtida no passo anterior:

Então, a altura da pipa relativa à pessoa é