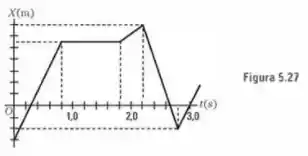
. A posição de um corpo em termos do tempo é dada na Fig. . Indicar: onde o movimento tem o sentido positivo do eixo e onde ele tem o sentido negativo; quando o movimento é acelerado e quando ele é retardado; quando o corpo passa pela origem; e quando a velocidade é zero. Fazer um esboço da velocidade e da aceleração como funções do tempo. Estimar, a partir do gráfico, a velocidade média entre e
, e , e .
Passo 1
Vem comigo que a gente detona com essa questão juntos!
Vamos avaliar cada item separadamente passo por passo, para que a gente não se perca e não tenha confusão. Vamos lá então!
Começando com o item .
Para o movimento estar no sentido positivo de a posição dele tem que estar crescendo na direção positiva desse eixo ou até mesmo parado em uma posição que faz parte do eixo positivo.
Olhando o gráfico vemos que isso acontece em e para .
Para o movimento estar no sentido negativo de a posição dele tem que estar crescendo na direção negativa desse eixo.
Olhando o gráfico vemos que isso acontece em .
Passo 2
Agora para o item .
Para um movimento ser acelerado ele tem que ter sofrido uma aceleração ou estar sofrendo uma que faz com ele adquira velocidade que faz com que ele se desloque para a direção positiva do eixo que estamos considerando.
E para um movimento ser retardado ele tem que ter sofrido uma aceleração ou estar sofrendo uma que faz com ele adquira velocidade que faz com que ele se desloque para a direção negativa do eixo que estamos considerando ou faça ele parar.
Sabendo disso e olhando no gráfico vemos que ele é acelerado instantaneamente em e em , já que ele começa a se movimentar na direção positiva do eixo .
E ele é retardado instantaneamente em e já quele no primeiro instante ele é parado, pois sua posição em se mantem constante e no segundo ele começa a se deslocar na direção negativa de .
Passo 3
Agora vamos para o item .
O corpo vai passar pela origem quando ele estiver em posição igual a zero, ou seja, quando ele encosta no eixo horizontal.
Olhando o gráfico isso acontece em dois instantes, em , e .
Passo 4
Agora para o último item, a letra .
A velocidade do corpo vai ser zero, quando sua posição não mudar com o tempo e pelo gráfico isso ocorre em .
Antes de montarmos o gráfico da velocidade me função do tempo, vamos achar a velocidade média entre os instantes onde temos mudança no comportamento do gráfico da posição, pois essas mudanças ocorrem poque a velocidade do corpo muda.
Podemos calcular essa velocidade média usando que:
Então para o instante , temos:
Para :
Para :
Para :
E para
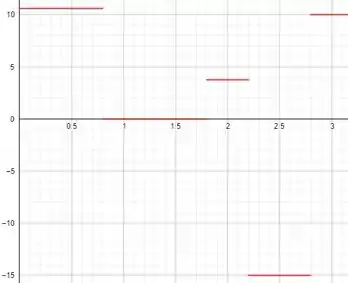
Com isso nosso esboço fica da seguinte forma:
Passo 5
Por último o enunciado quer que a gente encontre a velocidade média em alguns intervalos de tempo. Vamos usar a mesma coisa que usamos no passo anterior para achar velocidade média.
Assim para , temos:
Para , temos:
E para , temos:
Com isso a gente finaliza a questão com sucesso!
Resposta
Sentido positivo: e .
Sentido negativo: .
Acelerado: .
Retardado: e .
, e .
Velocidade zero: .
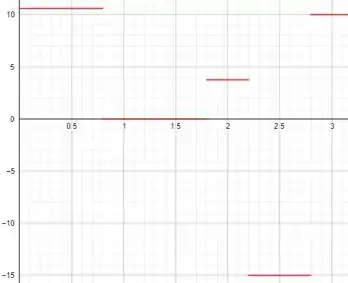
Cálculo das velocidades médias