48. Os Problemas e mostram diagramas de corpo livre de dois sistemas em interação. Para cada um deles, você deve

1. Redigir um problema realista para o qual o par de diagramas correspondente seja correto. Verifique se a resposta pedida no enunciado é realmente consistente com o que os diagramas mostram.
2. Resolva o problema proposto

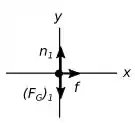
Vamos analisar o primeiro diagrama.

Forças verticais:

Primeira força vertical – A primeira força que vamos identificar nele é a força peso. Ela aponta na vertical para baixo e é dada por:

E no diagrama a gente pode ver que o valor da força peso é , sendo assim, para possuir esse valor . Ou seja, o primeiro diagrama representa um objeto com a massa de .

Segunda força vertical– A outra força vertical aponta verticalmente para cima e com o mesmo raciocínio anterior podemos ver que ela se trata da força normal.

Como a força normal e peso se cancelam não haverá nenhum movimento no eixo .

Forças horizontais:

Podemos ver que há apenas uma força horizontal, isso nos diz que esse objeto vai ter uma aceleração horizontal, mas não dá nenhuma informação sobre que força é essa, por enquanto.

Então, vamos seguir.

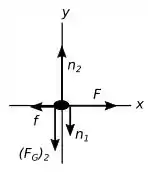
Agora vamos analisar o segundo diagrama.

Forças verticais:

Primeira força vertical – Uma coisa que podemos ver de cara é que o segundo diagrama possui uma força vertical para baixo com o mesmo valor da normal do diagrama anterior, e o que isso significa? Bom, significa que provavelmente formam um par ação/reação mas será que é possível? Vamos ver.

Vamos imaginar que os diagramas de forças representam dois blocos que vamos denominar de bloco e bloco . Se o bloco é o de massa , ou seja, e eles está acima do bloco então sim, as forças que estamos falando formam sim um par ação/reação.

Nosso problema está ganhando forma, então, vamos continuar.

Segunda força vertical – O segundo diagrama, que agora vamos chamar de diagrama do bloco , possui outra força vertical para baixo então podemos deduzir que essa força se trata da força peso. Sendo assim:

O segundo bloco possui massa de , ou seja,

Terceira força vertical – Bom, podemos ver que essa força que aponta verticalmente para cima é a soma das duas forças que apontam verticalmente para baixo, ou seja, podemos deduzir que essa força é a força normal do bloco .

Forças horizontais:

Primeira força horizontal – Essa primeira força é uma força que vai gerar um movimento no sistema formado pelos dois blocos, ou seja, podemos imaginar que essa força se trata de uma pessoa empurrando o bloco para direita com uma força . Certo?

Segunda força horizontal – Analisando a segunda força podemos ver que essa força horizontal para a esquerda possui o mesmo valor e sentido contrário da força horizontal do bloco , sendo assim elas são suspeitas de formar um par ação/reação. Mas em qual movimento isso será possível?

Bom, vamos supor que há atrito entre os dois blocos. Se há atrito o bloco ao fazer uma ação empurrando o bloco para trás sofre uma reação do bloco que é uma força para frente. Ou seja, ambas são forças de atritos que formam par ação/reação. Ou seja:

Agora que identificamos todas as forças, vamos montar um problema.

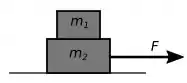
Vamos juntar todas informações que conseguimos e escrever bonitinho para definir um enunciado para o problema que ficará assim:

Um bloco de madeira de é colocado em cima de outro bloco de madeira de . Uma pessoa empurra o bloco de em uma superfície livre de atrito com uma força de . O bloco de na parte superior do bloco de irá deslizar?

Enfim podemos resolver o problema.

Para saber se o bloco vai ou não deslizar, vamos começar assumindo que os blocos irão se mover juntos com uma mesma aceleração .

Nosso primeiro passo será usar a segunda lei de Newton nos dois casos, porém como falamos nos passos anteriores as forças verticais vão se anular e não vão gerar aceleração vertical, sendo assim vamos aplicar a segunda lei só para as forças horizontais.

Bloco :

Bloco :

Precisamos descobrir , mas nós não sabemos quanto vale a aceleração, então precisamos descobri-la primeiro.

Vamos unir as duas equações anterior de modo que ficará:

Substituindo os valores que temos:

Agora vamos substituir essa aceleração em uma das equações no passo anterior para descobrir .

Essa é a força de atrito entre os blocos. (Olha, bateu certinho com o valor no diagrama, não é?)

Agora pra saber se ele desliza vamos descobrir a força de atrito estática máxima para esse problema. Sabemos que:

Substituindo os valores (sabendo que o coeficiente de atrito estático de madeira sobre madeira é tabelado):

Opa opa, , ou seja, desliza!