Seu professor de ciências lhe deu como tarefa construir um barômetro de água. Você aprendeu que a pressão da atmosfera pode variar em até de atmosfera padrão com as mudanças do clima.
a. Que altura mínima deve ter seu barômetro?
b. Em um dia de tempestade, o homem do tempo na TV diz que "a pressão barométrica esta tarde está reduzida em polegadas" . Qual é a altura da coluna de água do seu barômetro?
Passo 1
a) Podemos medir a pressão da atmosfera medindo a altura da coluna de líquido em um barômetro.
Bom! O barometro funciona assim...
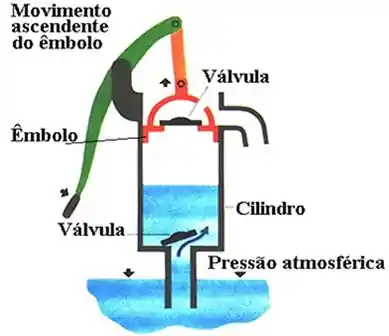
Aplicando o teorema de Stevin, temos que...
O que acontece é que lá em cima, no interior do barômetro, temos vácuo. De modo que, a pressão em é .
Como a pressão em é . Ficamos então, com...
Uma vez que é a densidade da água de , ficamos com...
Como a pressão da atmosfera pode variar em até de atmosfera, então...
Passo 2
b) Continuando nosso raciocínio, vamos agora pro segundo item!
Antes de mais nada, é importante saber que...
Sendo assim, uma vez que a pressão barométrica esta tarde está reduzida em polegadas, passando isso pra :
Pra obter a altura , basta seguir o mesmo esquema do item anterior...
Resposta
a)
b)