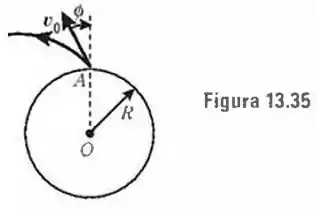
Um projétil balístico (Fig. ) de massa é lançado, de um ponto , com uma velocidade inicial , que faz um ângulo com a direção vertical ou radial. Calcule (a) o momento angular, (b) a energia total, (c) Prove que a excentricidade de sua órbita é dada por
[Sugestão: para (c), utilize o último resultado do Ex. .]
Passo 1
E aí, beleza?? Da questão anterior, sabemos que:
Assim, podemos escrever a energia e o momento angular como:
Passo 2
Portanto, vem:
Ou seja:
Como queríamos demonstrar.
Resposta
Ei, a resposta está no passo a passo :)