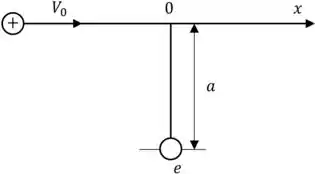
Um próton muito rápido com velocidade passa à distância de a elétron inicialmente em repouso (fig. 14- 53). Supondo que o movimento do próton não é perturbado devido à sua grande massa em relação à do próton, (a) faça o gráfico em função de x do componente da força perpendicular a que o próton exerce sobre o elétron. (b) Mostre que o momento transferido para o elétron é
em uma direção perpendicular a . (c) Estime o desvio do próton como uma função de sua velocidade. Este exemplo serve como base para analisar o movimento de partículas carregadas que passam por a matéria. [Dica: Supondo o elétron permanece praticamente em sua posição inicial enquanto o próton acontece, o momento transferido para o elétron é dado por e apenas a componente e perpendicular a tem que ser calculado. na visão de simetria de força, em vez de integrar de a , integrar de 0 a e multiplique por 2.]
Passo 1
Oiii tudo bem?
Vamos lá para mais um problema bem legal ein! Repetimos a figura do problema anterior:
Passo 2
A força exercida no ponto pode ser explicada como
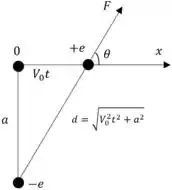
Passo 3
Podemos calcular o potencial elétrico como
Onde,
Passo 4
Para o campo elétrico temos:
Derivando em relação a
Passo 5
Para plotar o gráfico, chutamos alguns valores positivos e negativos para e ver qual valor de obtemos:
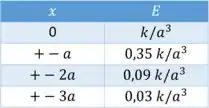
Podemos facilmente plotar o gráfico para esses dados
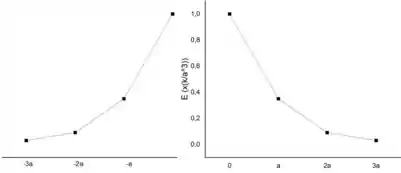
Passo 6
O calculo do momento é dado por