Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alonso e Finn - Mecânica- Ed: 2º - Capítulo 7.Problemas - Ex. 39

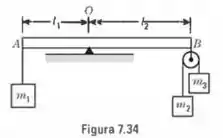
(a) Prove que a barra A B na Fig. 7.34 estará em equilíbrio se for satisfeita a equação

m 1 m 2 + m 3 l 1 = 4 m 2 m 3 l 2

b) Calcule a força que o ponto de apoio exerce na barra.

Passo 1

E aí, beleza?? O primeiro passo para resolver esse problema é calcular a tensão no fio da direita. Seja a a aceleração dos blocos 2 e 3 , vem:

m 2 g - T = m 2 a

T - m 3 g = m 3 a

Portanto:

g - T m 2 = T m 3 - g ∴ T = 2 m 2 m 3 g m 2 + m 3

Entretanto, o fio que liga B à barra possui o dobro da tensão, ou seja:

T ' = 2 T = 4 m 2 m 3 g m 2 + m 3

Passo 2

Equilibrando os torques em relação ao ponto O , vem:

m 1 g l 1 = T ' l 2

Portanto:

m 1 l 1 = 4 m 2 m 3 m 2 + m 3 l 2

Ou seja:

m 1 m 2 + m 3 l 1 = 4 m 2 m 3 l 2

Passo 3

Equilibrando as forças, vem:

N = m 1 g + T ' = m 1 + 4 m 2 m 3 m 2 + m 3 g = m 1 g 1 + l 1 l 2

N = m 1 g 1 + l 1 l 2

Resposta

N = m 1 g 1 + l 1 l 2

Ver Outros Exercícios desse livro