Prove que, se a energia cinética interna de um sistema de duas partículas é Et.cw o módulo das velocidades das partículas relativamente ao CM são:
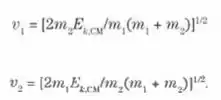
Passo 1
Falaa galera, tudo bem??
Como sabemos, para o centro de massa,
e que m1v1 = m2v2 = constante.
Assumindo movimento neste caso, temos:
Substituindo v1 na equação da energia cinética:
Agora conseguimos encontrar as equações para v1 e v2:
e
Resposta
Ei, a resposta está no passo a passo :)