Prove que, se é a resultante ele um sistema de forças concorrentes, e é o momento desse sistema em relação ao ponto , o momento, em relação ao ponto , é
Passo 1
E aí, beleza?? Vamos começar escrevendo a equação do torque em relação ao ponto :
Mas podemos escrever a localização de um ponto em relação ao ponto como:
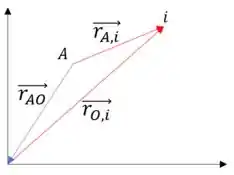
Passo 2
Portanto, vem:
Portanto, note que um dos termos corresponde ao torque total em relação à origem, enquanto o outro corresponde ao produto vetorial da posição de relativa a com a força resultante. Assim, vem:
Como queríamos demonstrar.
Resposta
Ei, a resposta está no passo a passo :)