Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.Problemas Adicionais - Ex. 114
Um raio luminoso parte do ponto A e chega ao ponto B depois de ser refletido no ponto O, situado na superfície de um espelho. Mostre, sem usar os métodos do cálculo, que a distância AOB é mínima quando o ângulo de incidência é igual ao ângulo de reflexão . (Sugestão: Considere a imagem de A no espelho.)
Passo 1
E aí meus caros(as)! A nossa missão agora é solucionar a questão 114!
Bem! E o que a gente tem aqui é um exerciciozinho sobre raios refletindo em espelhos!
Portanto, pra entender melhor o que tá acontecendo, vamo fazer um esboço da trajetória desse raio aí que saiu de e chegou em e da trajetória do raio que formou a imagem no espelho... O chamado ‘‘ Diagrama de raios’’!
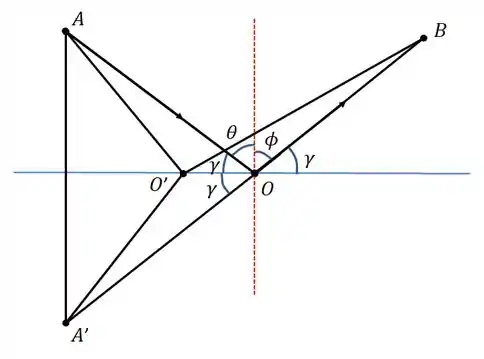
Da figura acima, a gente tira a seguinte relação...
Isso é a mesma coisa que dizer que...
Ou seja, o ângulo de incidência é igual ao ângulo de reflexão!
Passo 2
Para mostrar que é a distância mínima, vamos considerar um raio incidente com um raio refletido , tais que o ângulo de incidência não é igual ao ângulo de reflexão.
Logo, de acordo com a figura temos que...
Ou também podemos escrever isso aí em cima como...
Onde, pela desigualdade triangular...
E pode também ser reescrito como...
Logo, temos que...
Onde a desigualdade acaba vindo do fato de que a soma dos comprimentos de dois lados de um triângulo é sempre maior que o comprimento do terceiro lado