Repita os cálculos para o caso em que o braço esticado forma um angulo de , para baixo, com a horizontal.
Dados: distância cotovelo ombro = ; distância cotovelo pulso = ; e distância pulso centro da palma da mão = .
Passo 1
Esquematizando o braço para todo os pontos de rotação pedido para o exercício.
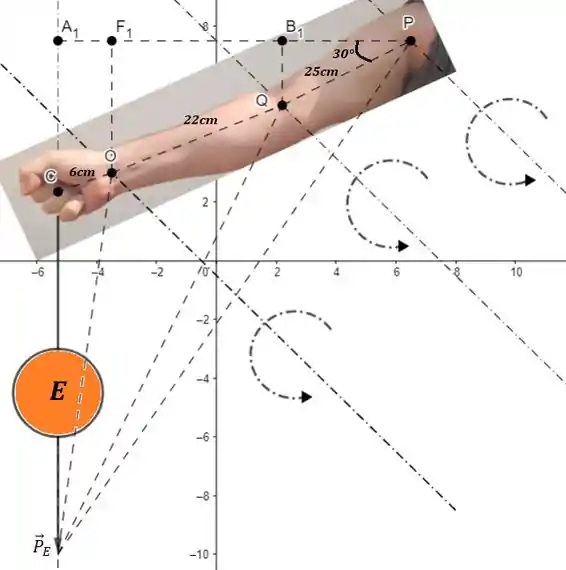
para resolver esse exercício, precisamos das distâncias perpendiculares ao ponto de rotação em cada membro:
Passo 2
Para o pulso:
Se arrastarmos o vetor força peso , até o ponto , a distância perpendicular ao ponto de giro do pulso ponto , é o segmento podemos determinar essa distância usando semelhança de triângulo.
E assim se estende para todo o exercício:
Os triângulos, são retângulos, temos as hipotenusas e um ângulo agudo, com essas informações determinaremos os segmentos, todos segmento contidos no segmento :
Passo 3
Para o segmento :
Passo 4
Para o segmento :
Passo 5
Para o segmento :
Passo 6
Agora que temos os valores de todos os segmentos podemos definir as distâncias perpendiculares ao ponto de giro de cada membro:
Passo 7
A distância da ação de até o ponto de rotação do pulso ponto , é :
Passo 8
A distância perpendicular da ação de até o ponto de rotação do cotovelo até ponto , é :
Passo 9
A distância perpendicular da ação de até o ponto de rotação do ombro até ponto , é :
Passo 10
Agora que temos todas as distâncias perpendiculares aos seus respectivos pontos de rotação definida, vamos calcular a força peso :
Adotando ;
Com isso definimos :
Passo 11
Agora com todos os valores definidos, vamos determinar os torques:
Torque no pulso:
Torque no cotovelo:
Torque no ombro:
Resposta
Para o pulso:
Para o cotovelo:
Para o ombro: