Um raio incide em um prisma de vidro no ar, de ângulo interno A=60°. O ângulo de incidência é tal que o raio emergente também faz um ângulo igual a com a normal a outra face.
a. Qual o índice de refração do vidro do prisma com relação ao ar?
b. Se o comprimento de onda da luz incidente for igual a 7000, qual será o da luz no interior do prisma, sabendo-se que sua frequência não muda?
Passo 1
a. Primeiramente devemos achar a relação entre os ângulos
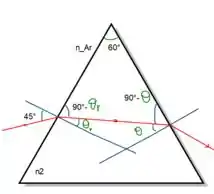
Da figura temos:
Logo,
Passo 2
Sabendo disso, podemos agora achar o ângulo
Da figura temos:
e usando que
Logo, aplicando na equação 1 do passo 1, temos:
Passo 3
b.
Usando que:
Como f= constante:
Resposta
a.
b.